bigraph-schema

bigraph-schema is a library to define schemas for and operate on bigraphical states, for use in composite biological simulations.

what is a bigraph?

A bigraph has three components - a set of nodes, a "place graph" over those nodes (a tree), and a "link graph" involving the same set of nodes (a hypergraph).

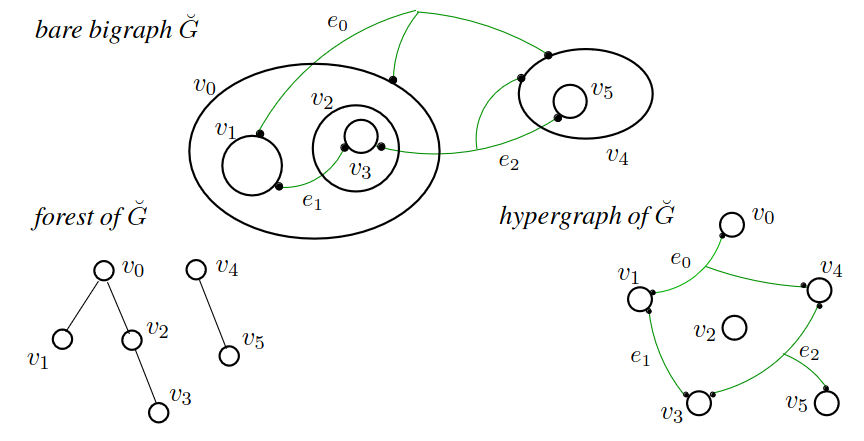
Bigraphs were invented by Robin Milner who made a series of "process calculi" culminating in bigraphs - he later implemented all of his previous process calculi as instances of bigraphs. Traditional "chemical reaction network" formalisms are instances of the π-calculus, the predecessor to bigraphs. Adding the tree (place graph) to the hypergraph allows us to express ideas of containment, nesting, and scale relationships, all critical things for biological applications. Also, even though the place and link graphs could be considered independent, their potential for interaction through shared nodes opens a new universe of relationships and transformations a system could embody.

reactions

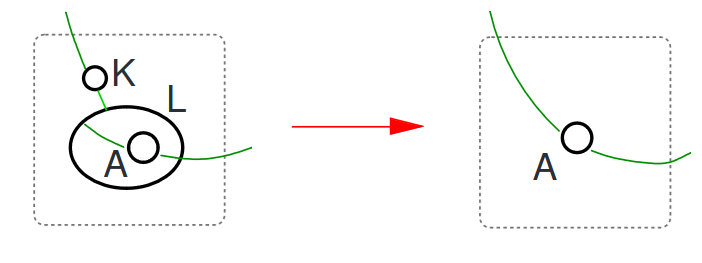
In addition to this structure, bigraphs are also capable of "motion" in the form of "reactions" - a pair of bigraphs used as a match and substitution respectively (known as the "redex" and the "reactum"). This means bigraphs update their structure and relationships over the course of a simulation.

Given a reaction that looks like this (the redex is on the left, reactum on the right):

and some bigraphical state that matches the redex of the reaction:

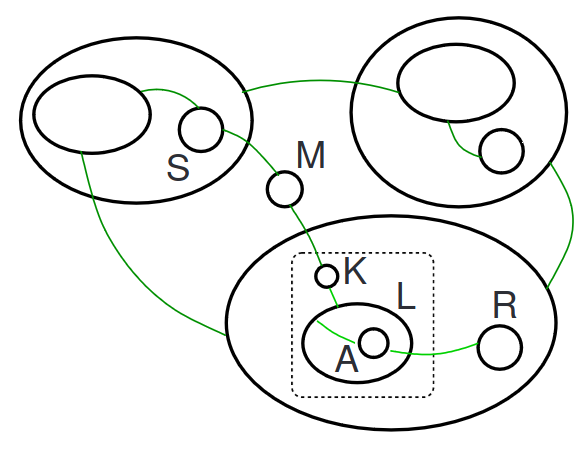
We can apply the reaction to the bigraph to achieve the resulting bigraph:

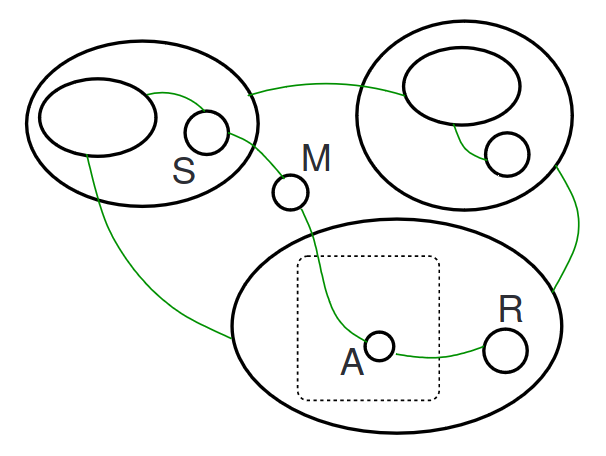
types

In addition to these core bigraphical properties, the states bigraph-schema works with are typed in a way that allows us to perform type-specific operations on values contained in the nodes or subtrees of the bigraph. Beyond providing these typed methods, the types also guide the composition of the larger systems out of smaller ones - edges are defined by the types of their inputs and outputs, so as we link our state together we can verify all of these connections are valid and make sense.

The way to declare the structure of types is by defining a "schema" - a nested state which describes the types of all the nodes embedded in the place graph. We will show how to define and use schemas throughout this notebook.

edges

An "edge" in bigraph-schema refers to a hyperedge which is defined by the types of its inputs and outputs - these two schemas together are the edge's "interface". Where the nesting of the schema reflects the "place" graph component of the bigraph, the edges encode the "link" graph, and these links themselves can be updated during the simulation. When using bigraph-schema in biological and general simulation applications, the hyperedges become "processes" which generate updates informed by the input states they are linked to, and these updates get applied to the output states the edge is linked to.

states and schemas

There is a distinction between a "schema", which encodes a description of states, and a "state", which holds the actual values which may or may not match any given schema. In bigraph-schema we need both of these things to perform any given operation - that said there are also methods to "infer" a given schema out of minimal type information provided in the state. In general there is a one to many relationship between a schema and states matching that schema - this gives us motivation to "register" schemas we use over and over again as new types, which will be described as well.

core

Let's start by importing the TypeSystem and creating an instance of it (codename core since we're going to use it a lot):

from bigraph_schema import TypeSystem
core = TypeSystem()

core uses a schema you provide to perform various operations on a given state or states. Let's see what types we have available:

core.types().keys()

dict_keys(['any', 'tuple', 'union', 'boolean', 'number', 'integer', 'float', 'string', 'list', 'tree', 'map', 'array', 'maybe', 'path', 'wires', 'schema', 'edge', 'length', 'time', 'current', 'luminosity', 'mass', 'substance', 'temperature', '', 'length/time', 'length^2*mass/time', 'current*time', 'length^2*mass/temperature*time^2', 'length/time^2', 'mass/length*time^2', 'current*time^2/length^2*mass', 'length^2*mass/current^2*time^3', '/substance', 'length^2*mass/substance*temperature*time^2', 'current*time/substance', 'current^2*time^3/length^2*mass', 'length^2*mass/current*time^2', 'mass/temperature^4*time^3', 'length^4*mass/time^3', 'length*temperature', '/temperature*time', 'length^3/mass*time^2', '/length', 'length*mass/current^2*time^2', 'current^2*time^4/length^3*mass', 'length^3*mass/current^2*time^4', 'length^2', '/time', 'length^3', 'length^3/time', 'length*mass/time^2', 'length^2*mass/time^2', 'length^2*mass/time^3', 'mass/length^3', 'mass/length*time', 'length^2/time', 'length*time/mass', 'substance/length^3', 'substance/time', 'length^2/time^2', 'current*time/mass', 'mass/time^2', 'luminosity/length^2', 'mass/time^3', 'length^2*mass/current*time^3', 'length*mass/current*time^3', 'current^2*time^4/length^2*mass', 'length^2*mass/current^2*time^2', 'mass/current*time^2', 'current*length*time', 'current*length^2*time', 'current*length^2', 'printing_unit', 'printing_unit/length', '/printing_unit', 'mass/length', 'length/mass', 'length^1_5*mass^0_5/time', 'length^0_5*mass^0_5/time', 'length^1_5*mass^0_5/time^2', 'mass^0_5/length^0_5*time', 'time/length', 'length^0_5*mass^0_5', 'mass^0_5/length^1_5', 'time^2/length'])

That's a lot of types! Looking through the list we see that most of them have to do with units - we'll get to unit types later, but for now we can see they are defined in terms of general notions (length or mass) rather than specific units (kilometer or gram) because we care about what is able to connect to what: for instance, all length units are compatible through scaling, that's the point of units!

basic types

Some of the basic types you probably already understand are:

• float: the computational equivalent of a real number - attempting to emulate a continuous number line with notable limitations.
• integer: positive and negative whole numbers.
• boolean: a two-valued type, here known as "true" and "false".
• string: a type for text, by default standard unicode.

Let's see what one of these types looks like - we'll take a simple one as an example, how about "float"? :

core.access('float')

{'_type': 'float',
 '_check': 'check_float',
 '_apply': 'accumulate',
 '_serialize': 'to_string',
 '_description': '64-bit floating point precision number',
 '_default': '0.0',
 '_deserialize': 'deserialize_float',
 '_divide': 'divide_float',
 '_inherit': ['number']}

We see here that types are defined through a series of keys, with any type specific information signified by key starting with an _ (underscore). Schemas and states in bigraph-schema claim the namespace of keys beginning with an underscore and reserves it for type information. A type may contain keys without underscores, but this signifies a subschema living under that key - in the end all the "leaves" of a schema tree resolve into type keys (keys with an underscore).

# a nested type with keys 'base' and 'state'
core.access({
    'base': 'integer', 
    'state': 'string'})

{'base': {'_type': 'integer',
  '_check': 'check_integer',
  '_apply': 'accumulate',
  '_serialize': 'to_string',
  '_description': '64-bit integer',
  '_default': '0',
  '_deserialize': 'deserialize_integer',
  '_inherit': ['number']},
 'state': {'_type': 'string',
  '_default': '',
  '_check': 'check_string',
  '_apply': 'replace',
  '_serialize': 'serialize_string',
  '_deserialize': 'deserialize_string',
  '_description': '64-bit integer'}}

What are all these keys?

Some, like _type, _definition, and _inherit, are information about the type itself. The others are all references to methods. Many of the methods in core rely on type-specific functions like this to operate, and we encode them as references to the function rather than a function itself to meet the requirement that our type descriptions are simply data and can be ie communicated across the network. This also allows the methods to be easily overridable to change behavior (_apply for instance we often want a different method here). This does rely on the definitions existing somewhere, and for the behavior of these functions to be sufficiently defined by tests for each method if the simulation is going to be replicated in another environment. We defer these considerations while providing now for their eventual resolution by insisting all values are serializable. This also allows for a future where the functions defining these methods are themselves somehow "universally" serializable, and instead of references we just store the serialized definition as the value.

• _type: This key is just the name of the type itself
• _check: This is the name of a function that the float type uses to verify some state is actually a float.
• _apply: The apply method takes two states which match the schema and returns some kind of "merge" of those states - it is up to each type method to determine what this means. Here we are using accumulate which just calls + on the two values. This works great if the values can be added. If not some other more sophisticated method would be required.
• _serialize, _deserialize: These are inverses of each other and are used to take complex values and turn them into something that can be communicated across the wire. One of the principles of bigraph-schema is that in order to operate in any distributed or multi-language environment, any state can be encoded as a string for the purposes of communication with other nodes in a large scale simulation. This principle is realized through a universal means of serialization and deserialization - all states are encodable and transmittable.
• _description: This allows anyone defining a type to explain what their type is all about.
• _default: If a value of this type is ever needed and no state information is provided, we deserialize the type's default value.
• _inherit: You can use existing types as a starting point to define new types. This relationship also helps us when merging schemas so that we can always select the most specific definition of each component of the resulting schema.

check

Let's take a look at how to use a schema now that we have one. First we can check different values to see if they match our schema:

core.check('float', 1.5)

True

core.check('float', 'not a float')

False

core.check('integer', 1.5)

False

core.check('integer', 5)

True

Let's do a few more but with a nested type.... we made one above (base/state keys) but don't want to have to retype it every time we want to use it. We can register a new type and then define schemas according to that:

# the keys 'base' and 'state' are part of the type
core.register(
    'histone', {
        'base': 'integer', 
        'state': 'string'})

# now it behaves like any other type
core.access('histone')

{'base': {'_type': 'integer',
  '_check': 'check_integer',
  '_apply': 'accumulate',
  '_serialize': 'to_string',
  '_description': '64-bit integer',
  '_default': '0',
  '_deserialize': 'deserialize_integer',
  '_inherit': ['number']},
 'state': {'_type': 'string',
  '_default': '',
  '_check': 'check_string',
  '_apply': 'replace',
  '_serialize': 'serialize_string',
  '_deserialize': 'deserialize_string',
  '_description': '64-bit integer'},
 '_type': 'histone'}

See how we still have the _type key on each leaf, but also a new _type key at the top level called histone. This is how you can form nested types.

Now we can call check with our newly registered type:

# not nested
core.check('histone', 5)

False

# nested but missing 'base' and 'state' keys
core.check('histone', {'c': 11})

False

# only one key, and wrong type anyway
core.check('histone', {'base': 'not a float'})

False

# right type, still missing the 'state' key
core.check('histone', {'base': 1111221})

False

# all the keys now, but 'state' is supposed to be a string
core.check('histone', {'base': 1111221, 'state': 5})

False

# here we go
core.check('histone', {'base': 1111221, 'state': 'M'})

True

# notably we can have more keys, as long as the ones in our schema match
core.check('histone', {'base': 1111221, 'state': 'M', 'c': 'this is okay'})

True

other methods

Okay, so now that we can check a state matches our schemas, what else can we do with them? There are a number of methods, here are a few:

• core.default(schema): generate the default value of a given schema.
• core.fill(schema, state): take an incomplete state and fill it with whatever is missing relative to the schema.
• core.complete(schema, state): given any schema fragment and state fragment, return as much of the state and schema as we are able to infer (kind of a bidirectional fill).
• core.de/serialize(schema, state): serialize a state according to the given schema so that it can later be recovered by deserialize.
• core.slice(schema, state, path): given a path into a state, slice into the state according to the schema.
• core.equivalent(schema, left, right): returns True if both left and right are equivalent states according to the given schema.
• core.apply(schema, state, update): given an existing state and an update that match a schema, return a state with that update applied according to the type system.
• core.view_edge(schema, state, path): transform the state into the form expected by an edge (residing at the given path) according to its current inputs state.
• core.project_edge(schema, state, path, view): transform a view in the form of an edge's outputs schema into states aligned with the edge's outputs state.
• core.match(schema, state, pattern): find instances of a pattern inside of the state.
• core.react(schema, state, reaction): apply a bigraphical reaction (redex/reactum) to a given state.
• core.fold(schema, state, method, values): fold a method over the state according to the schema, parameterized by a set of values.
• core.inherits_from(schema, descendant, ancestor): returns True if you can trace a path of inheritance from descendant schema to ancestor schema.
• core.resolve_schemas(schema, update): merges two schemas and returns the schema which has the most specific type of the two at each point in the schema.
• core.import_types(package): given a package containing a bundle of related types, register them all and make them available to ongoing operations.

This is a brief outline of these methods, let's go through a selection of them in more detail. But first, let's take make sure we understand type parameters.

type parameters

Basic types like float and string are atomic - they don't break down any further. The system allows for types with type parameters as well, which means the type itself is not complete until the parameter is specified, making it a complete type:

• list[element]: The element can be any other schema and defines the schema for each element in the list.
• map[value]: A map is a flat key/value store with the keys as strings and the value parameterized by whatever schema is in value.
• tree[leaf]: Tree is the recursive form of map whose values can themselves be trees or instances of the leaf type.
• tuple[0,1,...]: A tuple type has a specific number of elements and type for each element.
• array[tuple[0,1,...],data]: The array type can have arbitrary dimensions which are represented by a tuple of integers.
• maybe[value]: A maybe type can be the schema of its value or also be empty. If a type is not wrapped in maybe the system demands it has a value of the given schema at all times.
• union[0,1,...]: A union type is a collection of types the value could be. This works by checking each type one at a time and picking the first one that matches, so it matters the order you define the union to be.

How do these types work under the hood? Let's take a look at list, with a type parameter of boolean:

core.access('list[boolean]')

{'_type': 'list',
 '_default': [],
 '_check': 'check_list',
 '_slice': 'slice_list',
 '_apply': 'apply_list',
 '_serialize': 'serialize_list',
 '_deserialize': 'deserialize_list',
 '_fold': 'fold_list',
 '_divide': 'divide_list',
 '_type_parameters': ['element'],
 '_description': 'general list type (or sublists)',
 '_element': {'_type': 'boolean',
  '_default': False,
  '_check': 'check_boolean',
  '_apply': 'apply_boolean',
  '_serialize': 'serialize_boolean',
  '_deserialize': 'deserialize_boolean'}}

One thing we notice right away is that there's a lot of keys in here we didn't see in float: _slice, _fold, _divide, and also _type_parameters and _element, though maybe you can already tell what those are for. The first three are for additional methods the list type supports, while _type_parameters describes the kind of type parameters the type could have and the order they will appear in, where the values in the _type_parameters list indicate which additional keys will describe the actual type of those type parameters (in this case the element parameter, stored in the _element key). The value of the _element key in turn is the schema for boolean, exactly what we would need to know if we want to operate on each element in the list. If it had been a list[float] we had accessed, this would be the schema for float instead.

default

Get the default value of a given schema.... let's take a look at a few:

core.default('float')

0.0

core.default('string')

''

core.default('histone')

{'base': 0, 'state': ''}

fill

fill is kind of like default except it uses as much of a given state as it is able to:

core.fill('histone', {'state': 'M'})

{'state': 'M', 'base': 0}

This is useful to take partial states and fill them in with a complete schema to initialize a simulation, for instance.

paths and slice

One of the benefits of the "place" graph is that we can work with addresses (or "paths") into the tree to find or mark specific nodes for further computation. In order to traverse the tree to a given path you can use core.slice():

directory = {
    'root': {
        'bin': {
            'run'},
        'home': {
            'you': {
                'data': 5}}}}

# navigate through the tree to find whatever lives at the given path
data_schema, data = core.slice(
    'tree[integer]', 
    directory, 
    ['root', 'home', 'you', 'data'])

data

5

Here we see that slice also returns the schema it finds at the node the path points to. This can be used for further core operations local to that node.

path is also a type:

core.access('path')

{'_type': 'path',
 '_default': [],
 '_check': 'check_list',
 '_slice': 'slice_list',
 '_apply': 'apply_path',
 '_serialize': 'serialize_list',
 '_deserialize': 'deserialize_list',
 '_fold': 'fold_list',
 '_divide': 'divide_list',
 '_type_parameters': ['element'],
 '_description': 'general list type (or sublists)',
 '_element': {'_type': 'string',
  '_default': '',
  '_check': 'check_string',
  '_apply': 'replace',
  '_serialize': 'serialize_string',
  '_deserialize': 'deserialize_string',
  '_description': '64-bit integer'},
 '_inherit': ['list[string]']}

We see it inherits from list[string] - it receives all the methods from list and has it's _element pre-filled with the schema for string. This means we can use it for any other core operations:

core.check('path', 5)

False

core.default('path')

[]

core.check('tree[path]', {'a': {'b': ['a', 'x']}, 'x': {'y': ['b']}})

True

core.fill({'a': 'tree[path]', 'z': 'float'}, {'a': {'b': ['a', 'x']}, 'x': {'y': ['b']}})

{'a': {'b': ['a', 'x']}, 'x': {'y': ['b']}, 'z': 0.0}

edges

There is a special type in bigraph-schema called an edge which represents the hyperedges from the "link" graph in bigraph theory. Each edge is defined by its "interface" - the schema for its inputs and outputs. Once the interface is defined, it can be wired, or "linked" into the graph by providing a set of paths.

Let's make an edge schema to use as an example for various things:

edge_schema = {
    '_type': 'edge',
    '_inputs': {
        'concentration': 'float',
        'field': 'map[boolean]'},
    '_outputs': {
        'target': 'boolean',
        'total': 'integer',
        'delta': 'float'}}

Great, let's see what it looks like when we access this.... in general the access will unfold the type to its maximal form, recursively looking up each type definition and substituting it in. That's why the output looks so verbose:

core.access(edge_schema)

{'_type': 'edge',
 '_inputs': {'concentration': 'float', 'field': 'map[boolean]'},
 '_outputs': {'target': 'boolean', 'total': 'integer', 'delta': 'float'},
 '_default': {'inputs': {}, 'outputs': {}},
 '_apply': 'apply_edge',
 '_serialize': 'serialize_edge',
 '_deserialize': 'deserialize_edge',
 '_check': 'check_edge',
 '_type_parameters': ['inputs', 'outputs'],
 '_description': 'hyperedges in the bigraph, with inputs and outputs as type parameters',
 'inputs': {'_type': 'wires',
  '_default': {},
  '_check': 'check_tree',
  '_slice': 'slice_tree',
  '_apply': 'apply_tree',
  '_serialize': 'serialize_tree',
  '_deserialize': 'deserialize_tree',
  '_fold': 'fold_tree',
  '_divide': 'divide_tree',
  '_type_parameters': ['leaf'],
  '_description': 'mapping from str to some type in a potentially nested form',
  '_leaf': {'_type': 'path',
   '_default': [],
   '_check': 'check_list',
   '_slice': 'slice_list',
   '_apply': 'apply_path',
   '_serialize': 'serialize_list',
   '_deserialize': 'deserialize_list',
   '_fold': 'fold_list',
   '_divide': 'divide_list',
   '_type_parameters': ['element'],
   '_description': 'general list type (or sublists)',
   '_element': {'_type': 'string',
    '_default': '',
    '_check': 'check_string',
    '_apply': 'replace',
    '_serialize': 'serialize_string',
    '_deserialize': 'deserialize_string',
    '_description': '64-bit integer'},
   '_inherit': ['list[string]']},
  '_inherit': ['tree[path]']},
 'outputs': {'_type': 'wires',
  '_default': {},
  '_check': 'check_tree',
  '_slice': 'slice_tree',
  '_apply': 'apply_tree',
  '_serialize': 'serialize_tree',
  '_deserialize': 'deserialize_tree',
  '_fold': 'fold_tree',
  '_divide': 'divide_tree',
  '_type_parameters': ['leaf'],
  '_description': 'mapping from str to some type in a potentially nested form',
  '_leaf': {'_type': 'path',
   '_default': [],
   '_check': 'check_list',
   '_slice': 'slice_list',
   '_apply': 'apply_path',
   '_serialize': 'serialize_list',
   '_deserialize': 'deserialize_list',
   '_fold': 'fold_list',
   '_divide': 'divide_list',
   '_type_parameters': ['element'],
   '_description': 'general list type (or sublists)',
   '_element': {'_type': 'string',
    '_default': '',
    '_check': 'check_string',
    '_apply': 'replace',
    '_serialize': 'serialize_string',
    '_deserialize': 'deserialize_string',
    '_description': '64-bit integer'},
   '_inherit': ['list[string]']},
  '_inherit': ['tree[path]']}}

One thing we can see about an edge is that it has both inputs and outputs keys, and _inputs and _outputs (with underscores) as well. What is going on here?

One clue is that the _type_parameters list for the _edge type is ['inputs', 'outputs'], which means edge is a type with two type parameters, _inputs and _outputs. This explains the underscore keys, they are the actual schemas for these type parameters, defining what type of edge this is.

The other keys are inputs and outputs states and have their own subschema, which match the names of the type parameters by design but ultimately only by convention. The subschemas for these states are of type wires, which itself inherits from tree[path]. Wires are how we link together the "ports" of each edge (its inputs and outputs schemas) with actual places in the tree matching those types.

An example will be helpful, and we can introduce another core method, complete(), which is like a bidirectional fill that is aware of edges and how type constraints propagate through wires. Here is an example edge state we can use:

edge_state = {
    'inputs': {
        'concentration': ['molecules', 'glucose'],
        'field': ['states']},
    'outputs': {
        'target': ['states', 'growth'],
        'total': ['emitter', 'total molecules'],
        'delta': ['molecules', 'glucose']}}

The form of the keys here is the same as the schema, an inputs and outputs key with subkeys, but the values are different. Here all the types have been replaced by paths. These are the places in the tree where we will "link" one of the ports of this edge according to the input and output schemas.

complete

Type constraints can come from many places. We can put them directly in the schema and in that way enforce what kind of states are allowed. We can also supply type hints in the form of _type and associated type parameter keys in the state itself to generate the right schema that fits the state. Type constraints can also flow from edges whose wires tell us that something that matches its interface must live wherever that path is pointing. To call upon all these kinds of type inference we can appeal to core.complete(), which takes all of this into account:

full_schema, full_state = core.complete(
    {'edge': edge_schema},
    {'edge': edge_state, 'molecules': {'glucose': 10.0}})
full_state

{'edge': {'inputs': {'concentration': ['molecules', 'glucose'],
   'field': ['states']},
  'outputs': {'target': ['states', 'growth'],
   'total': ['emitter', 'total molecules'],
   'delta': ['molecules', 'glucose']}},
 'molecules': {'glucose': 10.0},
 'states': {'growth': False},
 'emitter': {'total molecules': 0}}

full_schema

{'edge': {'_type': 'edge',
  '_inputs': {'concentration': 'float', 'field': 'map[boolean]'},
  '_outputs': {'target': 'boolean', 'total': 'integer', 'delta': 'float'},
  '_default': {'inputs': {}, 'outputs': {}},
  '_apply': 'apply_edge',
  '_serialize': 'serialize_edge',
  '_deserialize': 'deserialize_edge',
  '_check': 'check_edge',
  '_type_parameters': ['inputs', 'outputs'],
  '_description': 'hyperedges in the bigraph, with inputs and outputs as type parameters',
  'inputs': {'_type': 'wires',
   '_default': {},
   '_check': 'check_tree',
   '_slice': 'slice_tree',
   '_apply': 'apply_tree',
   '_serialize': 'serialize_tree',
   '_deserialize': 'deserialize_tree',
   '_fold': 'fold_tree',
   '_divide': 'divide_tree',
   '_type_parameters': ['leaf'],
   '_description': 'mapping from str to some type in a potentially nested form',
   '_leaf': {'_type': 'path',
    '_default': [],
    '_check': 'check_list',
    '_slice': 'slice_list',
    '_apply': 'apply_path',
    '_serialize': 'serialize_list',
    '_deserialize': 'deserialize_list',
    '_fold': 'fold_list',
    '_divide': 'divide_list',
    '_type_parameters': ['element'],
    '_description': 'general list type (or sublists)',
    '_element': {'_type': 'string',
     '_default': '',
     '_check': 'check_string',
     '_apply': 'replace',
     '_serialize': 'serialize_string',
     '_deserialize': 'deserialize_string',
     '_description': '64-bit integer'},
    '_inherit': ['list[string]']},
   '_inherit': ['tree[path]']},
  'outputs': {'_type': 'wires',
   '_default': {},
   '_check': 'check_tree',
   '_slice': 'slice_tree',
   '_apply': 'apply_tree',
   '_serialize': 'serialize_tree',
   '_deserialize': 'deserialize_tree',
   '_fold': 'fold_tree',
   '_divide': 'divide_tree',
   '_type_parameters': ['leaf'],
   '_description': 'mapping from str to some type in a potentially nested form',
   '_leaf': {'_type': 'path',
    '_default': [],
    '_check': 'check_list',
    '_slice': 'slice_list',
    '_apply': 'apply_path',
    '_serialize': 'serialize_list',
    '_deserialize': 'deserialize_list',
    '_fold': 'fold_list',
    '_divide': 'divide_list',
    '_type_parameters': ['element'],
    '_description': 'general list type (or sublists)',
    '_element': {'_type': 'string',
     '_default': '',
     '_check': 'check_string',
     '_apply': 'replace',
     '_serialize': 'serialize_string',
     '_deserialize': 'deserialize_string',
     '_description': '64-bit integer'},
    '_inherit': ['list[string]']},
   '_inherit': ['tree[path]']}},
 'molecules': {'glucose': {'_type': 'float',
   '_check': 'check_float',
   '_apply': 'accumulate',
   '_serialize': 'to_string',
   '_description': '64-bit floating point precision number',
   '_default': '0.0',
   '_deserialize': 'deserialize_float',
   '_divide': 'divide_float',
   '_inherit': ['number'],
   'molecules': {'glucose': {'edge': {'_type': 'edge',
      '_inputs': {'concentration': 'float', 'field': 'map[boolean]'},
      '_outputs': {'target': 'boolean', 'total': 'integer', 'delta': 'float'},
      '_default': {'inputs': {}, 'outputs': {}},
      '_apply': 'apply_edge',
      '_serialize': 'serialize_edge',
      '_deserialize': 'deserialize_edge',
      '_check': 'check_edge',
      '_type_parameters': ['inputs', 'outputs'],
      '_description': 'hyperedges in the bigraph, with inputs and outputs as type parameters',
      'inputs': {'_type': 'wires',
       '_default': {},
       '_check': 'check_tree',
       '_slice': 'slice_tree',
       '_apply': 'apply_tree',
       '_serialize': 'serialize_tree',
       '_deserialize': 'deserialize_tree',
       '_fold': 'fold_tree',
       '_divide': 'divide_tree',
       '_type_parameters': ['leaf'],
       '_description': 'mapping from str to some type in a potentially nested form',
       '_leaf': {'_type': 'path',
        '_default': [],
        '_check': 'check_list',
        '_slice': 'slice_list',
        '_apply': 'apply_path',
        '_serialize': 'serialize_list',
        '_deserialize': 'deserialize_list',
        '_fold': 'fold_list',
        '_divide': 'divide_list',
        '_type_parameters': ['element'],
        '_description': 'general list type (or sublists)',
        '_element': {'_type': 'string',
         '_default': '',
         '_check': 'check_string',
         '_apply': 'replace',
         '_serialize': 'serialize_string',
         '_deserialize': 'deserialize_string',
         '_description': '64-bit integer'},
        '_inherit': ['list[string]']},
       '_inherit': ['tree[path]']},
      'outputs': {'_type': 'wires',
       '_default': {},
       '_check': 'check_tree',
       '_slice': 'slice_tree',
       '_apply': 'apply_tree',
       '_serialize': 'serialize_tree',
       '_deserialize': 'deserialize_tree',
       '_fold': 'fold_tree',
       '_divide': 'divide_tree',
       '_type_parameters': ['leaf'],
       '_description': 'mapping from str to some type in a potentially nested form',
       '_leaf': {'_type': 'path',
        '_default': [],
        '_check': 'check_list',
        '_slice': 'slice_list',
        '_apply': 'apply_path',
        '_serialize': 'serialize_list',
        '_deserialize': 'deserialize_list',
        '_fold': 'fold_list',
        '_divide': 'divide_list',
        '_type_parameters': ['element'],
        '_description': 'general list type (or sublists)',
        '_element': {'_type': 'string',
         '_default': '',
         '_check': 'check_string',
         '_apply': 'replace',
         '_serialize': 'serialize_string',
         '_deserialize': 'deserialize_string',
         '_description': '64-bit integer'},
        '_inherit': ['list[string]']},
       '_inherit': ['tree[path]']}},
     'molecules': {'glucose': {...}},
     'states': {'_type': 'map',
      '_default': {},
      '_apply': 'apply_map',
      '_serialize': 'serialize_map',
      '_deserialize': 'deserialize_map',
      '_check': 'check_map',
      '_slice': 'slice_map',
      '_fold': 'fold_map',
      '_divide': 'divide_map',
      '_type_parameters': ['value'],
      '_description': 'flat mapping from keys of strings to values of any type',
      '_value': {'_type': 'boolean',
       '_default': False,
       '_check': 'check_boolean',
       '_apply': 'apply_boolean',
       '_serialize': 'serialize_boolean',
       '_deserialize': 'deserialize_boolean'},
      'growth': {'_type': 'boolean',
       '_default': False,
       '_check': 'check_boolean',
       '_apply': 'apply_boolean',
       '_serialize': 'serialize_boolean',
       '_deserialize': 'deserialize_boolean'}},
     'emitter': {'total molecules': {'_type': 'integer',
       '_check': 'check_integer',
       '_apply': 'accumulate',
       '_serialize': 'to_string',
       '_description': '64-bit integer',
       '_default': '0',
       '_deserialize': 'deserialize_integer',
       '_inherit': ['number']}}}}}},
 'states': {'_type': 'map',
  '_default': {},
  '_apply': 'apply_map',
  '_serialize': 'serialize_map',
  '_deserialize': 'deserialize_map',
  '_check': 'check_map',
  '_slice': 'slice_map',
  '_fold': 'fold_map',
  '_divide': 'divide_map',
  '_type_parameters': ['value'],
  '_description': 'flat mapping from keys of strings to values of any type',
  '_value': {'_type': 'boolean',
   '_default': False,
   '_check': 'check_boolean',
   '_apply': 'apply_boolean',
   '_serialize': 'serialize_boolean',
   '_deserialize': 'deserialize_boolean'},
  'growth': {'_type': 'boolean',
   '_default': False,
   '_check': 'check_boolean',
   '_apply': 'apply_boolean',
   '_serialize': 'serialize_boolean',
   '_deserialize': 'deserialize_boolean'}},
 'emitter': {'total molecules': {'_type': 'integer',
   '_check': 'check_integer',
   '_apply': 'accumulate',
   '_serialize': 'to_string',
   '_description': '64-bit integer',
   '_default': '0',
   '_deserialize': 'deserialize_integer',
   '_inherit': ['number']}}}

view and project

The point of edge interfaces is that the process designer shouldn't need to worry how their process is going to be wired in to a particular simulation, they can define the behavior of the update(inputs, interval) method in terms of its inputs and outputs schema in a simple and idealized form and let the wiring allow it to fit in any (type-matching) way with respect to a given structured state.

Along these lines, we need a way to "view" a state from the perspective of an edge and its inputs, and also to "project" the outputs from the form the edge defined to the one implied by its outputs.

Here are the input paths for our edge, ie the mapping from how the process sees the values it operates on to the actual places in the state where those values live.

full_state['edge']['inputs']

{'concentration': ['molecules', 'glucose'], 'field': ['states']}

When we "view" the state we receive it in the form the edge expects based on its schema and inputs:

core.view_edge(full_schema, full_state, ['edge'])

{'concentration': 10.0, 'field': {'growth': False}}

When instead we "project" we are taking a state that's produced by the edge according to its outputs schema and translating that back into wherever the output paths are pointing in the total state:

full_state['edge']['outputs']

{'target': ['states', 'growth'],
 'total': ['emitter', 'total molecules'],
 'delta': ['molecules', 'glucose']}

projection = core.project_edge(
    full_schema, 
    full_state, 
    ['edge'], 
    {'target': True, 'total': 55, 'delta': -0.001})
projection

{'states': {'growth': True},
 'emitter': {'total molecules': 55},
 'molecules': {'glucose': -0.001}}

apply

So what can we do with view_edge and project_edge? We can formulate inputs into the edge from the surrounding state in the perspective the edge expects (view), the edge can perform some computation on it, produce an update in the form of its outputs, then translate that back into the original form of the outer state (project, which could be totally different as long as the types of each of the ports match). Once we have an update in the form of the outer state we can "apply" that update back onto the original state, thereby incorporating into the simulation state a change contributed by one of the edges in that simulation. By iterating this you can perform an entire simulation, producing a timeseries of structure and states that can be further analyzed or composed with other simulations.

As an example, let's use the projection of the update we computed above:

core.apply(
    full_schema, 
    full_state, 
    projection)

{'edge': {'inputs': {'concentration': ['molecules', 'glucose'],
   'field': ['states']},
  'outputs': {'target': ['states', 'growth'],
   'total': ['emitter', 'total molecules'],
   'delta': ['molecules', 'glucose']}},
 'molecules': {'glucose': 9.999},
 'states': {'growth': True},
 'emitter': {'total molecules': 55}}

In this case we see the apply added the update to the existing value. Sometimes this is what we want (this is the meaning of the "accumulate" apply method) and sometimes its not. We can also override any of the methods in the schema (notice the original full_state is unchanged - applying an update always leaves the original state alone):

full_state

{'edge': {'inputs': {'concentration': ['molecules', 'glucose'],
   'field': ['states']},
  'outputs': {'target': ['states', 'growth'],
   'total': ['emitter', 'total molecules'],
   'delta': ['molecules', 'glucose']}},
 'molecules': {'glucose': 10.0},
 'states': {'growth': False},
 'emitter': {'total molecules': 0}}

full_schema['molecules']['glucose']['_apply'] = 'set'
core.apply(full_schema, full_state, projection)

{'edge': {'inputs': {'concentration': ['molecules', 'glucose'],
   'field': ['states']},
  'outputs': {'target': ['states', 'growth'],
   'total': ['emitter', 'total molecules'],
   'delta': ['molecules', 'glucose']}},
 'molecules': {'glucose': -0.001},
 'states': {'growth': True},
 'emitter': {'total molecules': 55}}